Разбор самостоятельной работы
1. Напишите функцию, которая подсчитывает количество единичных битов в данном четырёхбайтном целом числе. Функция должна быть оптимизирована по скорости и использовать возможно меньше памяти.
Первый способ:
int bitCounter(int N) {
int count = 0;
for (int i = 0; i < 32; i++) {
count += N & 1;
N = N >>> 1; //можно было и так: N = N >> 1;
}
return count;
}
Возможно, выражение
N & 1
кажется менее понятным, чем выражение
N % 2.
Но второе выражение при отрицательных N считает не то, что нам нужно. Минус этого алгоритма заключается в том,
что каждый раз функция совершает одно и тоже число операций. Вне зависимости от числа N проверяются все его биты.
Второй способ:
int bitCounter(int N) {
int count = 0;
while (N != 0) {
count += N & 1;
N = N >>> 1; //а здесь нельзя N = N >> 1;
}
return count;
}
Стоит обратить внимание на побитовый сдвиг вправо без сохранения знака. Если бы мы сдвигали, сохраняя знак, то для отрицательных чисел этот цикл был бы бесконечным.
Плюсы этого алгоритма:
- – в случае положительных чисел, функция не будет проверять последние нулевые биты.
- – не требуется счётчик i, и, следовательно, с ним не выполняются операции сравнения и увеличения на единицу.
Третий способ:
int bitCounter(int N) {
int count = 0;
while (N != 0) {
count++;
N = N & (N-1); //удаляет последнюю единицу
}
return count;
}
Поясним этот алгоритм на примере.
| выражение | двоичный вид |
|---|---|
N | <какие-то биты>1000 |
N-1 | <те же биты>0111 |
N & (N - 1) | <те же биты>0000 |
Операция N & (N - 1)
не меняет битов перед первой единицей справа, а её саму обнуляет. Таким образом, будет совершено столько
итераций цикла, сколько единичных битов в числе. То есть, в среднем, 16 итераций. Этот алгоритм явно быстрее предыдущих двух.
Какой же лучше выбрать? Конечно, первый и второй способы понятнее. А третий быстрее. Но множество проектов умирает, не родясь, от так называемой преждевременной оптимизации. Стоит писать программу так, как приходит в голову, а потом, если окажется что она недостаточно быстро работает, искать тонкие места и оптимизировать (если вдруг этим местом будет подсчёт битов в байте, то тогда использовать третий алгоритм).
Четвёртый способ:
int bitCounter(int N) {
N = (N & 0x55555555) + ((N >>> 1) & 0x55555555);
N = (N & 0x33333333) + ((N >>> 2) & 0x33333333);
N = (N & 0x0F0F0F0F) + ((N >>> 4) & 0x0F0F0F0F);
N = (N & 0x00FF00FF) + ((N >>> 8) & 0x00FF00FF);
N = (N & 0x0000FFFF) + ((N >>> 16) & 0x0000FFFF);
return N;
}
Поясним первую строчку.
Разобьём число на два. Первое число совпадает с искомым числом в чётных битах,
а его все его нечётные равны нулю. Чётные биты второго числа совпадают с нечётными битами искомого, а все его нечётные
равны нулю. Как же их получить? Получим первое число вот таким образом:
N & 0x55555555.
Так как число 0x55555555 имеет вид 0101 0101 0101 0101 0101 0101 0101 0101 0101 0101, результатом такой операции действительно
будет первое число. Чтобы получить второе
число, применим к исходному числу сдвиг на один бит вправо и применим побитовое И с тем же числом 0х55555555. Таким образом,
мы получим второе число. Чтобы стало понятнее, рассмотрим конкретный пример:
| Выражение | Его значение |
|---|---|
N | 0110 0100 1000 1001 1110 0011 1110 1111 |
N & 0x55555555 | 0100 0100 0000 0001 0100 0001 0100 0101 |
(N >> 1) & 0x55555555 | 0001 0000 0100 0100 0101 0001 0101 0101 |
N = (N & 0x55555555) + ((N >> 1) & 0x55555555) | 0101 0100 0100 0101 1001 0010 1001 1010 |
N = (N & 0x33333333) + ((N >> 1) & 0x33333333) | 0010 0001 0001 0010 0011 0010 0011 0100 |
N = (N & 0x0F0F0F0F) + ((N >> 1) & 0x0F0F0F0F) | 0000 0011 0000 0011 0000 0101 0000 0111 |
N = (N & 0x00FF00FF) + ((N >> 1) & 0x00FF00FF) | 0000 0000 0000 0110 0000 0000 0000 1100 |
N = (N & 0x0000FFFF) + ((N >> 1) & 0x0000FFFF) | 0000 0000 0000 0000 0000 0000 0001 0010 |
Теперь сложим этих два числа. Если рассматривать
полученное число по паре
битов(01 01 01 00 01 00 01 01 10 01 00 10 10 01 10 10), то в каждой паре битов записано количество единичных битов ,
которое было на их местах в числе до преобразования. Итак:
N = (N & 0x55555555) + ((N >>> 1) & 0x55555555).
Теперь применим аналогичные манипуляции, но уже к парам битам получившегося числа:
N = (N & 0x33333333) + ((N >>> 2) & 0x33333333).
В каждой четвёрке битов полученной суммы (0010 0001 0001 0010 0011 0010 0011
0100) записано количество единичных битов, которое было на их местах в числе до преобразований.
Совершим третье преобразование:
N = (N & 0x0F0F0F0F) + ((N >>> 4) & 0x0F0F0F0F). Теперь в каждой восьмерке битов (00000011 00000011 00000101 00000111) записано количество
единичных битов, которое было на их местах в числе до преобразований.
Четвёртое преобразование:
N = (N & 0x00FF00FF) + ((N >>> 4) & 0x00FF00FF).
Каждая группа из шестнадцати битов полученного числа (0000000000000110 0000000000001100) представляет собой количество
единичных битов, которое было на их местах в числе до преобразования.
Ну и завершающее преобразование:
N = (N & 0x0000FFFF) + ((N >>> 4) & 0x0000FFFF)
.
Мы получили количество единичных битов в искомом числе 0000 0000 0000 0000 0000 0000 0001 0010 = 18.
Таким образом, чтобы посчитать число единичных битов в четырёхбайтовом целом числе, потребовалось ровно 5 операций.
Знание этого метода наизусть имеет сомнительную ценность, поскольку на практике вряд ли встретится эта задача, но имеются другие ценности:
- – если вы поняли этот алгоритм, то это было полезное упражнение.
- – на интервью эта задача встречается довольно часто, поэтому алгоритм полезно знать.
Автоматически такой алгоритм писать в программах не стоит, поскольку это будет преждевременной оптимизацией.
2. Напишите функцию, которая подсчитывает количество единичных битов в данном очень длинном (скажем, из миллиарда элементов) массиве байтов. Функция должна быть оптимизирована по скорости.
В этой задаче есть два почти равноценных решения.
1) завести таблицу
int table[256],
которую заранее заполнить. В
table[i]
будет храниться число единичных битов в байте, где i — номер байта. Причём под номером байта мы понимаем его численное
значение. Во время работы функции, пробегая
по элементам массива, мы будем просто обращаться к элементам массива и прибавлять их значения к искомой сумме.
2) написать большой switch:
switch (bt) {
case 0: return 0;
case 1: return 1;
case 2: return 1;
...
}
Если алгоритмы будут реализованы на языке С, то разницы по времени не будет. А вот если они будут реализованы на языке Java, то второй будет быстрее, поскольку в первом Java будет каждый раз проверять, не выходим ли мы за пределы таблицы (а это два сравнения).
Стандартные структуры данных.
Рассказывать про алгоритмы и структуры данных сложно. Поначалу некоторые ученики не понимают, что не главное в программировании выучить какой-то язык. После этого некоторые думают, что главное научиться писать алгоритмы. Но этот этап с развитием программирования становится всё менее существенным. В реальности же большинство стандартных алгоритмов уже написано. Почти все стандартные структуры данных и алгоритмы есть в стандартных библиотеках языков программирования.
В этой главе будет рассказано, как они написаны, но это не означает, что все их вы должны написать. Кто же такие стандартные структуры данных?
В первую очередь «очевидные» структуры данных, которые в Java называются примитивными типами, и массивы.
Но у массива должно быть заранее (в момент создания) известно число элементов. Мы рассмотрим структуры данных, которые решают этот недостаток.
1. «Массив переменной длины» (линейные структуры данных).
Что можно сделать с массивом:
| Операция | Псевдокод |
|---|---|
| создать | A = new int[200]; |
| взять элемент по индексу | A[i] |
| записать в элемент по индексу | A[i] = |
| узнать длину массива | length |
При создании массива, в памяти выделяется сплошной кусок памяти нужного размера, в котором элементы массива идут по порядку. И изменить длину массива нельзя, поскольку соседний кусок памяти может быть уже занят. Мы хотим получить аналог, но чтобы длину можно было менять по дороге. Что нам хочется уметь делать с этим массивом:
- – создать (массив нулевой длины)
- – добавить ещё один элемент в конец массива
- – узнать длину массива
- – взять элемент по индексу
- – изменить элемент по заданному индексу
- – добавить элемент по индексу
- – удалить элемент по индексу
Как его можно реализовать?
Варианты реализаций:
Список.
Чтобы избежать проблемы фиксированной длины массива, будем хранить каждый элемент нашего списка (например, содержащего целые числа), как пару: int и указатель на следующий элемент. С такой реализацией не будет проблем с добавлением.
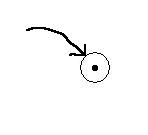
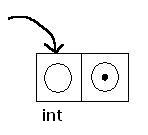
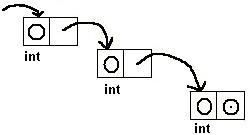
Заводим где угодно элемент и ставим указатель на него. Как будут выглядеть операции в списке и какое у них будет время работы:
| Операция | Время работы |
|---|---|
| Создание: создание нулевого указателя. | О(1) |
| Добавление ещё одного элемента в конец массива: если массив пустой, то создаём элемент и делаем так, чтобы начало массива указывало на него. | Если мы будем хранить не только указатель на начало списка, но и на конец, то эта операция будет выполняться за константное время (так реализовано в Java), а если только на начало, то время работы будет O(N). |
| Узнать длину массива. | пробегаем по массиву до указателя в никуда, считая количество элементов. Время работы в таком случае порядка N. В Java дополнительно хранится длина, поэтому эта операция выполняется за константное время. |
| Взятие элемента по индексу. | Пробегаем по списку до нужного элемента. Время работы O(index). |
| Изменение элемента по заданному индексу. | O(index) |
| Добавление элемента по индексу. | O(index) |
| Удаление элемента по индексу. | O(index) |
Рассмотрим, как это реализуется в Java на примере списка с целыми числами. В Java 5.0 есть такой тип
LinkedList<Integer>.
Чтобы его использовать, надо написать такую строчку в начале файла: import java.util.LinkedList; а чтобы им пользоваться:
| Операция | Синтаксис |
|---|---|
| создание переменной | LinkedList<Integer> list; |
| инициализация | list = new LinkedList<Integer>(); |
| добавление элемента в конец списка | list.add(25); |
| длина массива | list.size(); |
| проверка на пустоту | list.isEmpty(); |
| взятие элемента по индексу | list.get(index); |
| изменение элемента по индексу | list.set(index, value); |
| добавление элемента по индексу | list.add(index, value); |
| удаление элемента по индексу | list.remove(index); |
Есть ещё методы, но мы рассмотрим дополнительно только один: часто требуется перебрать все элементы в массиве. Например, нам нужна их сумма. Мы можем реализовать её так:
for (int i = 0; i < list.size(); ++i)
sum += list.get(i);
}
Этот метод работает за время O(size2). Почему? Чтобы взять первый элемент требуется 1 операция, чтобы второй 2, и т. д. 1+2+…+length = length(length+1)/2. Это очень долго. Кроме того, крайне неразумно (если только значение функции не меняется во время выполнения цикла) использовать в условии цикла вызов функции. Если нам нужно её значение, то стоит поступить следующим образом:
int length = list.size(); for (int i = 0; i < length; ++i) …
Но даже это существенно не улучшит время работы. В Java есть такая возможность (начиная с версии 5.0. В версиях 1.4. она тоже есть, только запись сложнее):
for ( int i : list) { //для всех элементов списка
sum += i; //прибавляем их всех к сумме
}
Этот алгоритм работает за линейное время O(size).

