Алгоритмы сортировки.
Зачем нужно знать, как структуры данных устроены внутри?
- Чтобы выбирать для использования наиболее подходящие из них.
- Зная устройство уже известных структур данных, легче писать новые.
Зачем нужно знать алгоритмы?
- Алгоритмы ценны как упражнения.
- Хитрые алгоритмы приводят к новым структурам данных.
Задача сортировки.
Дана линейная структура данных (чаще всего массив) из объектов, которые можно сравнивать. Расположить объекты в порядке возрастания.
[2, 5, 3, 8, 1] => [1, 2, 3, 5, 8]
(1) Алгоритмы, работающие за время O(N2).
Сортировка вставками.
Цель: отсортировать начальный кусок задачи.
шаг 1: [2, 5, 3, 8, 1] шаг 2: [2, 5, 3, 8, 1] (отсортированы первые 2 элемента массива) шаг 3: [2, 3, 5, 8, 1] (отсортированы первые 3 элемента массива) ...
Реализация:
Для каждого i от 2 до N {
1) сравниваем i-й элемент по очереди с 1-м, 2-м, ..., (i-1)-м;
2) находим, куда его нужно вставить (время в среднем ~i/2);
3) вставляем элемент (время в среднем ~i/2)
}
Однако данный алгоритм имеет явный недостаток: в уже отсортированном массиве он также работает за время ~N2. Чтобы этого избежать, будем сравнивать элемент с предыдущими в обратном порядке, т. е.:
1*) сравниваем i-й элемент по очереди с (i-1)-м, (i-2)-м, ..., 1-м;
Сортировку вставками полезно применять к небольшим массивам
Сортировка пузырьком.
Повторить N-1 раз {
для каждого i от 1 до N-1 {
если (A[i] > A[i+1]), то меняем их местами;
}
}
Время работы ~(N-1)*(N-1), что есть O(N2).
В отсортированном массиве этот алгоритм работает также за O(N2). Однако его можно улучшить:
- прохождение по массиву имеет смысл повторять только до тех пор, пока за каждое такое прохождение мы выполняем хотя бы одну перестановку элементов.
- очевидно, что за i шагов мы переставим в конец i наибольших элементов массива в отсортированном порядке, поэтому на каждом шаге мы можем пробегать не весь массив, а только неотсортированную его часть (N-i первых элементов)
Таким образом, улучшенный алгоритм выглядит так:
K = N - 1;
Повторять {
для каждого i от 1 до K {
если (A[i] > A[i+1]), то меняем их местами;
}
K--;
} пока была хоть одна перестановка.
(2) Пирамидальная сортировка (HeapSort)
Пирамида — двоичное дерево, в котором каждый родитель не меньше своих сыновей.
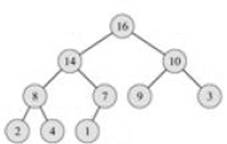
Пусть на основе входного массива нам удалось построить пирамиду. Тогда легко найти максимальный элемент (он находится в корне дерева). Этот элемент можно поместить в конец выходного массива, а в корень перенести последний из листьев.
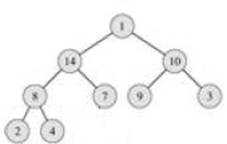
Теперь нам нужно восстановить свойство пирамиды. Для этого меняем корень с наибольшим из его сыновей:
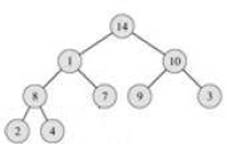
Однако свойство опять не выполнено. Поэтому опять меняем узел, для которого оно не выполнено, с наибольшим из его сыновей и повторяем эту операцию, пока не получим пирамиду:
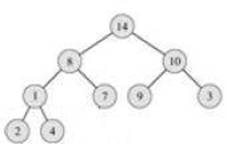
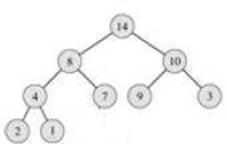
Теперь мы опять можем взять максимум и поставить его в выходной массив на предпоследнее место и т.д.
Каждый такой шаг выполняется в худшем случае за время ~log2K, где K — кол-во элементов в пирамиде. Т. о. в худшем случае все шаги выполнятся за время log2N + log2(N-1) + ... + log21, и т. к.
Nlog2N > log2N + log2(N-1) + ... + log21 > log2(1*N) + log2(2*N) + ... > N/2*log2N,
то время сортировки массива при уже построенной на его основе пирамиде есть O(Nlog2N).
Остаётся вопрос: как построить пирамиду?
Запишем элементы массива в узлы двоичного дерева по порядку. Начинаем проверять выполнение свойства пирамиды с предпоследнего уровня (для листьев оно, очевидно, выполнено). Если для какого-то узла свойство не выполнено, то опускаем его вниз по дереву, меняя его каждый раз с наибольшим из сыновей, пока для поддерева, в котором он был корнем, не будет выполнено свойство пирамиды.
Сколько времени займёт такая процедура? В худшем случае:
0*2k-1 + 1*2k-2 + 2*2k-3 + ... + (i-1)*2k-i + ... + 20*(k-1), где k — кол-во уровней в дереве (k~log2N).
Эту сумму (обозначим её S) можно посчитать двумя способами:
1) S = 2k-2 + 2k-3 + ... + 1 +
2k-3 + ... + 1 +
...
+ 1 = (2k-1 - 1) + (2k-2 -1) + ... + (2-1) =
= 2k - 2 - (k -1) = 2k - k - 1;
2) S = 2S - S = 2k-1 + 2k-2 + ... + 2 - (k-1) =
= 2k - 2 - (k-1) = 2k - k - 1 ~ N - log2N - 1 ~ N
Таким образом, время построения пирамиды линейно, а значит время всего алгоритма сортировки ~Nlog2N.
Куча
Когда речь идёт о структуре данных, пирамиду обычно называют кучей.
Операции:
- построить из массива — за время O(N);
- взять максимум — O(1);
- удалить максимум и перестроить — O(log2N)
С помощью кучи можно быстро сделать частичную сортировку (например, переставить в конец массива несколько наибольших его элементов)
Замечательное свойство кучи.
У элемента массива с номером i детьми будут элементы с номерами 2i и 2i-1. Это означает, что кучу можно хранить в самом исходном массиве, то есть не использовать для неё дополнительную память.
(3) QuickSort
Идея этого алгоритма состоит в том, чтобы выбрать средний элемент в массиве, поставить его на своё место, меньшие элементы перенести влево от него, а большие — вправо, и затем рекурсивно отсортировать каждую из половинок.
Предположим, что середину мы можем выбрать за время ~N, где N — длина массива. Тогда на k-ом шаге у нас получится порядка 2k частей, в каждой из которых середина ищется за ~N/2k, то есть на каждый шаг уходит время ~N. И т.к. для того, чтобы придти к частям длины 1 понадобится порядка log2N шагов, то время работы сортировки в лучшем случае ~Nlog2N.
Как выбрать элемент, который разделит массив на две части?
Возьмём первый элемент в массиве и заведём два счётчика: первый всегда указывает на наш элемент, а второй сначала указывает на последний элемент массива и движется всегда по направлению к первому. На каждом шаге сравниваем элементы, на которые указывают счётчики. Если они стоят в неправильном порядке, то меняем их местами и двигаем второй счётчик. И так до тех пор, пока счётчики не совпадут
[5(1), 1, 6, 2, 7(2)] => [5(1), 1, 6, 2(2), 7] => [2, 1 (2), 6, 5(1), 7] =>...=> [2, 1, 5(1,2), 6, 7]
Если на каждом шаге выбирать середину неудачно, то время работы увеличится до ~N2. При этом отсортированный массив является наихудшим случаем.
В среднем же случае сортировка работает за время O(Nlog2N) (пока без док-ва)
- В классе java.util.Arrays метод sort реализован следующим образом: если размер массива не превосходит 8, то используется сортировка вставками, иначе QuickSort.
(4) MergeSort
Делим массив пополам, сортируем каждую часть рекурсивно и затем сливаем получившиеся массивы в один. Например,
[1, 5, 7, 22], [2, 4, 6, 8] [] [5, 7, 22], [2, 4, 6, 8] [1] [5, 7, 22], [4, 6, 8] [1, 2] [5, 7, 22], [6, 8] [1, 2, 4] ...
Останавливаемся, когда один из массивов становится пустым, оставшуюся часть другого записываем в конец.
Слияние происходит за время ~N, и так на каждом шаге делим массив пополам, то шагов log2N, след-но MergeSort работает за время O(Nlog2N) в любом случае.
Однако этот алгоритм использует дополнительную память, и потому не всегда удачен. Но, например, в случае, когда в массиве хранятся ссылки на объекты, размер дополнительной памяти невелик. Поэтому в классе java.util.Collections сортировка реализована с помощью MergeSort.
ТЕОРЕМА.
Не существует алгоритма сортировки, работающего в среднем быстрее O(Nlog2N).
Док-во.
Пусть имеется N различных объектов. Существует N! их различных перестановок.
Предположим, что существует алгоритм, работающий быстрее O(Nlog2N). Представим его в виде последовательности операций и бинарных ветвлений. Получим двоичное дерево. Тогда работу алгоритма можно представить, как проход по этому дереву от корня до какого-нибудь листа. Причём каждой перестановке соответствует свой собственный маршрут, то есть в дереве существует как минимум N! листьев. В лучшем случае (если дерево сбалансировано: если дерево не сбалансировано, то сбалансировав его, уменьшим среднюю длину маршрута) каждый маршрут будет иметь длину log2N! ~ Nlog2N, след-но среднее время работы никак не меньше O(Nlog2N).
(5) RadixSort (сортирует только числа)
Сортируем числа сначала по последней цифре (разбиваем массив на 10 частей, соответствующие разным цифрам, и в конце соединяем их), потом по предпоследней и т.д. На k-м шаге мы отсортируем числа по последним k цифрам. На последнем шаге соответственно получим отсортированный массив
[1233, 2132, 1131, 1211, 2112, 2333] [1131, 1211, 2132, 2112, 1233, 2333] [1211, 2112, 1121, 2132, 1233, 2333] [2112, 1121, 2132, 1211, 1233, 2333] [1121, 1211, 1233, 2112, 2132, 2333]
Сортировка по одной цифре занимает время ~O(N), кол-во цифр в числах — константа. Сортировка работает за время O(N)
В чём же противоречие с теоремой?
На самом деле, если мы попытаемся отсортировать с помощью RadixSort N различных чисел, то наибольшее из них будет иметь как минимум [log10N] + 1 цифр ([] — целая часть), то есть ~log2N цифр. А значит, сама сортировка будет работать не менее Nlog2N.
Обратная задача
Вместе с задачей сортировки часто рассматривают в некотором смысле обратную ей задачу, а именно:
Задача.
Имеется упорядоченный массив длины N. Построить алгоритм, который с равной вероятностью выдаёт каждую из N! перестановок элементов массива.
Рассмотрим два алгоритма, работающие линейное время:
(1) for (i = 0; i < N; i++) {
поменять A[i] и A[RANDOM(0..N-1)];
}
(2) for (i = 0; i < N; i++) {
поменять A[i] и A[RANDOM(i..N-1)];
}
Докажем правильность второго алгоритма.
С равной вероятностью на первом месте у нас может оказаться один из N элементов, на втором — один из N-1 оставшихся, и т.д. Всего получаем N! равновероятных перестановок. Но они все различны, так как перестановок исходного массива тоже N! и при этом каждую мы можем получить с помощью алгоритма, если нам повезёт каждый раз ставить на i-е место нужный элемент. А значит алгоритм корректен.
В то же время первый алгоритм очевидно неверен, так как в нём мы имеем NN вариантов работы алгоритма и NN в общем случае на N! не делится, след-но мы не можем говорить о равновероятности получения любой перестановки.

