Алгоритмы сортировки.

Постановка задачи:
Дано: структура данных, состоящая из объектов, которые можно сравнивать.
Нужно: расставить эти объекты в возрастающем порядке.

В качестве структуры данных рассмотрим массив длины N, состоящий из чисел. (Элементы массива будем нумеровать с 1.)

I. Медленные алгоритмы

1. Сортировка вставками

На i-м шаге сортировки получаем массив, где элементы с 1-го по (i + 1)-й расположены по возрастанию.

Пример:
Дано: 2 6 5 3 1 4, N = 6
Шаг 1: 2 6 5 3 1 4
Шаг 2: 2 5 6 3 1 4
Шаг 3: 2 3 5 6 1 4
Шаг 4: 1 2 3 5 6 4
Шаг 5: 1 2 3 4 5 6

Оценим время работы алгоритма.

На каждом шаге время требуется, во-первых, на поиск места для вставки i-го элемента при сортировке массива длины i + 1, а, во-вторых, на сдвиг элементов, начиная со стоящего на месте, куда вставляем новый элемент, по (i - 1)-й элемент на одну позицию вправо.

Вставка: 1 способ. Сравниваем i-й элемент поочередно с 1-м, 2-м,..., (i - 1)-м. До момента, когда i-й элемент оказывается меньше либо равным тому, с которым сравниваем. В среднем, на это уходит i / 2 операций.

Сдвиг: в среднем сдвигаем i / 2 элементов.

Вставка и сдвиг повторяются (N - 1) раз. (Число шагов.)

Таким образом, время работы пропорционально N². (1 + 2 + : + (N - 1))

Насколько быстро этот алгоритм справляется с уже отсортированным массивом?

Т. к. при выборе места вставки каждый элемент сравнивается последовательно с 1ым, 2ым,.., то время пропорционально N².

Но его можно улучшить, если делать вставку способом 2. Сравниваем i-й элемент поочередно с (i - 1)-ым, (i - 2)-ым,.., 1-м. Тогда на отсортированном массиве на каждом шаге будет производиться лишь одно сравнение (с (i - 1)-м элементом), а вставка и сдвиг не потребуются. Следовательно, время в данном случае линейно.

Безусловный плюс этого алгоритма — его простота. Он хорош для небольших по длине массивов. Например, в Java встроенная сортировка в случае, если длина массива меньше 8, использует именно алгоритм сортировки вставками, а в остальных - более сложные алгоритмы.

2. Сортировка "пузырьком"

На каждом шаге пробегаем по всему массиву, сравнивая соседние элементы. В случае, если они стоят не по возрастанию, меняем их местами. Таким образом, после первого шага максимальный элемент окажется на последнем месте. После второго - второй по величине элемент окажется на своем, предпоследнем, месте, и т. д. Следовательно, потребуется (N - 1) шаг.

Пример:
Дано: 2 5 3 1 4, N = 5
Шаг 1: 2 5 3 1 4 -> 2 5 3 1 4 -> 2 3 5 1 4 -> 2 3 1 5 4 -> 2 3 1 4 5
Шаг 2: 2 3 1 4 5 -> 2 3 1 4 5 -> 2 1 3 4 5 -> 2 1 3 4 5 -> 2 1 3 4 5
Шаг 3: 2 1 3 4 5 -> 1 2 3 4 5 -> 1 2 3 4 5 -> 1 2 3 4 5 -> 1 2 3 4 5
Шаг 4: 1 2 3 4 5 -> 1 2 3 4 5 -> 1 2 3 4 5 -> 1 2 3 4 5 -> 1 2 3 4 5

Время работы.

Алгоритм работает в среднем за О(N²). ((N - 1) шагов по (N - 1) сравнение)

Насколько быстро он справляется с уже отсортированным массивом?

При такой реализации как раз за О(N²).

Но это время можно улучшить, если вместо фиксированного числа шагов повторять действия до тех пор, пока в теле цикла была сделана хоть одна перестановка. Тогда на отсортированном массиве алгоритм будет работать за линейное время. (Потребуется всего одна итерация.)

Кроме того, можно еще улучшить наш алгоритм: на i-м шаге пробегать не по всему массиву, а лишь от первого элемента до (N + 1 - i)-го.

II. Пирамидальная сортировка (HeapSort)

Пирамида — это двоичное дерево с числами в узлах, обладающее свойством пирамиды: значение каждого ребенка не превосходит значения своего родителя.

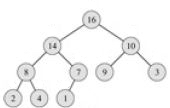
Если нам удастся построить по исходному массиву пирамиду, то максимальный элемент массива   ее корень.

Допустим, что пирамида построена. И она сбалансирована. (Этого можно добиться, последовательно заполняя слева направо элементами уровни дерева, начиная с уровня, на котором находится корень) Вынем из нее корень и запишем на его место крайний правый лист. (В нашем примере его значение равно 1.)

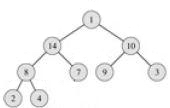
После этого восстановим свойство пирамиды следующим способом: поменяем местами корень и сына с максимальным значением.

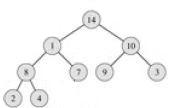
Перейдем на второй уровень. Рассмотрим поддерево, в котором после первого шага нарушилось свойство пирамиды, и выполним для него аналогичные действия, и т. д., пока не дойдем до листа.

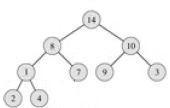
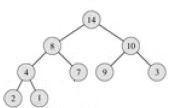
Такое восстановление потребует порядка logN операций (logN   высота сбалансированного дерева).

Время работы.

Подсчитаем время сортировки, при условии, что пирамида построена.

Каждый раз вынимаем из пирамиды корень (максимум), записываем его в конец массива. После этого восстанавливаем свойство пирамиды:
(*) logN + log(N - 1) + ... + log1, где N, N - 1, ..., 1 — количество оставшихся в куче элементов.

Заметим, что сумма (*) не меньше суммы своих первых [N / 2] членов, а значение каждого из них не меньше log[N / 2].

Заметим также, что значение каждого из членов суммы (*) не превосходит значения первого члена (logN).

Таким образом, получаем оценки для суммы (*) : [N / 2] log[N / 2] <= (*) <= NlogN.

Левая и правая часть пропорциональны NlogN, следовательно, и сумма (*) пропорциональна NlogN.

Осталось научиться изготавливать из массива пирамиду.

Будем строить пирамиду следующим образом. Возьмем числа массива и сложим в дерево в произвольном порядке. Тогда в листьях (пусть это будет k-тый уровень) свойство пирамиды нарушено не будет. Пройдем по (k - 1)-ому уровню, исправляя ошибки, затем по (k - 2)-ому и т. д., пока не придем в корень.

При этом на каждом уровне мы восстанавливаем свойство пирамиды в поддеревьях, где оно нарушено лишь в корне.

Подсчитаем время, требующееся на построение пирамиды.

S = 0 * 2^{k - 1} + 1 * 2^{k - 2} + 2 * 2^{k - 3} + ... + (i - 1) * 2^{k - i} + ... + (k - 1) * 2⁰ , где 2^{k - i} — количество элементов на (k-i)-том уровне, i - 1 — количество исправлений.

Пусть S = x, тогда 2x = 0 * 2^{(k - 1) + 1} + ... + (i - 1) * 2^{(k - i) + 1} + ... + (k - 1) * 2¹ =
= 1 * 2^{(k - 1)} + : + j * 2^{(k - j)} + : + (k - 1) * 2¹ =
= ( 0 * 2^{(k - 1)} + : + (j - 1) * 2^{(k - j)} + : + (k - 1) * 2¹ ) + ( 2^{(k - 1)} + ... + 2^{(k - j)} + ... + 2¹ ) =
= x - (k - 1) + 2^k - 2 = x + 2^k - k - 1.

Таким образом, x = 2^k - k - 1, где k = logN — количество листьев.

Следовательно, на построение пирамиды требуется N - logN - 1, т. е. O(N) времени.

Таким образом, пирамидальная сортировка работает за О(NlogN).

Куча.

Введем понятие кучи. Куча — это структура данных, которая:
- быстро строится из массива (O(N))
- в ней быстро берется максимальный элемент (О(1))
- можно удалить максимальный элемент (О(NlogN))

С помощью кучи легко решается задача нахождения первых k наибольших элементов в массиве.

Как хранить кучу в массиве?

В качестве вершин кучи будем рассматривать ячейки массива. Детьми элемента с индексом i будут элементы с индексами 2i и 2i + 1. Индекс родителя находится по формуле [i / 2].

При сортировке, беря из кучи максимум, будем переставлять его с последним листом. Таким образом, дополнительной памяти не потребуется.

III.QuickSort

Поделим массив на две части так, чтобы значение каждого из элементов левой не превосходило значения центрального элемента, а значение каждого из элементов правой части было не меньше значения центрального. Этого можно добиться за O(N) операций.

Произведем аналогичные операции с левой и правой половиной массива(O(N / 2) и O(N / 2). Итого O(N)). Потом с четвертинками и т. д.

Всего потребуется logN шагов.

Время работы.

Таким образом, при условии, что каждый раз удается выбрать средний по значению элемент, алгоритм работает за O(NlogN).

Как разделить массив на две части?

Способ 1: возьмем в качестве центрального элемент, стоящий в массиве на первом месте. Заведем два счетчика, первый из которых будет указывать на выбранный нами элемент, а второй — на конец массива. Будем двигать счетчик, указывающий не на выбранный нами элемент, в сторону сближения с другим счетчиком, сравнивая значения элементов, на которые они указывают и, если нужно, меняя эти элементы местами. Будем продолжать процесс до совпадения счетчиков.

Пример:
3(1) 2 4 5 0 1(2) -> 1 2(1) 4 5 0 3(2) -> 1 2 4(1) 5 0 3(2) -> 1 2 3(1) 5 0(2) 4 -> 1 2 0 5(1) 3(2) 4 -> 1 2 0 3(1, 2) 5 4

Но при таком способе на отсортированном массиве (первый элемент всегда наименьший) каждый раз он разбивается на части длин 1 и N_i - 1, где N_i — длина массива на i - м шаге. Таким образом, потребуется N - 1 шаг, а время работы будет пропорционально N².

Чтобы избежать такого "невезения" на отсортированном массиве, можно, например, каждый раз брать элемент со средним значением индекса в качестве центрального.

В Java встроенная сортировка использует для массивов длины больше 8 элементов QuickSort, в котором центральный элемент выбирается как средний по значению из 9 элементов, равномерно расположенных по массиву.

Таким образом, QuickSort в лучшем случае работает за O(NlogN), а в худшем за О(N²).

В среднем случае он также работает за O(NlogN).

IV. MergeSort

Делим массив пополам, сортируем отдельно левую и правую части, затем сливаем их в один массив.

Пример слияния:

Заводим в каждом массиве указатель на первый элемент, сравниваем значения элементов, на которые они указывают, и меньший элемент перекладываем в новый массив, сдвигая соответствующий указатель на единицу вправо. Когда один из массивов заканчивается, перекладываем оставшиеся во втором массиве элементы в конец общего массива.

1(1) 5 7 22;    2(2) 4 6 8
1 5(1) 7 22;    2(2) 4 6 8;   общий массив: 1
1 5(1) 7 22;    2 4(2) 6 8;   общий массив: 1 2
1 5(1) 7 22;    2 4 6(2) 8;   общий массив: 1 2 4
1 5 7(1) 22;    2 4 6(2) 8;   общий массив: 1 2 4 5
1 5 7(1) 22;    2 4 6 8(2);   общий массив: 1 2 4 5 6
1 5 7 22(1);    2 4 6 8(2);   общий массив: 1 2 4 5 6 7
1 5 7 22(1);    2 4 6 8   ;   общий массив: 1 2 4 5 6 7 8
1 5 7 22   ;    2 4 6 8   ;   общий массив: 1 2 4 5 6 7 8 22

Время работы.

Одно слияние выполняется за O(длины общего результирующего массива). Всего слияний порядка logN. Итого, время работы алгоритма во всех случаях О(NlogN).

Но минус этого алгоритма состоит в том, что он, в отличие от вышеперечисленных, требует дополнительной памяти на общие результирующие массивы.

Для масcива элементов примивного типа занимаемая память удваивается, в случае массива объектов нужно продублировать только ссылки, т. е. дополнительная используемая память в отношении к уже занимаемой невелика.

В стандартной библиотеке Java для сортировки массива объектов как раз используется MergeSort.

Теорема.

Не существует алгоритма, в среднем сортирующего структуру данных из N объектов быстрее, чем за О(NlogN).

Доказательство.

Сортируем N различных объектов, следовательно, существует N! их различных перестановок, т. е. N! различных входных данных.

Рассмотрим программу, сортирующую структуры данных длины N. Представим ее в виде последовательности операций и бинарных ветвлений, т. е. сопоставим ей бинарное дерево.

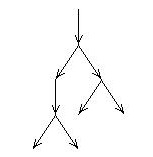
Сортировке каждого из наборов входных данных однозначно сопоставляется маршрут в дереве от корня до одного из N! листьев.

Высота дерева, имеющего N! листьев, будет минимальной, если оно сбалансировано. В этом случае его высота равна log(N!), т. е. пропорциональна NlogN. (log(N!) = logN + log(N-1) + ... + log1 ~ NlogN (доказывалось в подсчете времени работы HeapSort). Это и означает, что программа не может в среднем сортировать структуру данных из N объектов быстрее, чем за О(NlogN).

V. RadixSort

Пример:

1233
2132
1131
1211
2112
2333

Будем сортировать N чисел следующим образом. Отсортируем их по последней цифре. Это потребует O(N) операций.

1131
1211
2132
2112
1233
2333

Заметим, что числа, у которых последняя цифра совпадает, сохранили относительно друг друга порядок следования.

Теперь отсортируем их по предпоследней цифре. (O(N)).

1211
2112
1131
2132
1233
2333

и т. д.

2112
1131
2132     
1211
1233
2333

1131
1211
1233
2112
2132
2333

Каждая из сортировок по i-й цифре занимает O(N) времени. Всего сортировок конечное число, таким образом, RadixSort работает за O(N), что противоречит теореме.

На самом деле, это не так. Противоречия с теоремой нет. Мы сортируем N чисел. Допустим, они все различны, тогда длина самого большое из них должна быть не менее logN.

Отсюда следует, что на самом деле сортировок не конечное число, а О(logN), и алгоритм работает за О(NlogN).

Перестановки

Мы рассмотрели алгоритмы сортировки массивов, но иногда возникает противоположная задача: перемешать массив. Формальнее, требуется процедура, с равной вероятностью выдающая все N! возможных перестановок элементов массива длины N.

Рассмотрим два алгоритма, работающих за линейное время.

1)
for (i = 0; i < N; i++) {
  swap(a[i], a[RANDOM(0:N - 1)]);
}

Процедура swap меняет в массиве местами свои аргументы, а RANDOM(0:N - 1) с равной вероятностью выдает значения от 0 до N - 1. Таким образом, после i-го шага на i-м месте стоит случайное число.

2) 
for (i = 0; i < N; i++) {
  swap(a[i], a[RANDOM(i:N - 1)]);
}

Докажем правильность второго алгоритма.

Алгоритм имеет N! различных исходов. (На нулевом шаге имеется N вариантов значения для 0-го элемента, на первом N - 1 (значения всех элементов массива, кроме 0-го), на втором N - 2 и т. д.) Вероятность каждого исхода 1 / N!. Таким образом, с равной вероятностью могут быть получены все N! различных перестановок.

Докажем неправильность первого алгоритма.

Алгоритм имеет N^N различных исходов. N^N, как правило, не делится на N!, из чего следует, что не все исходы равновероятны.